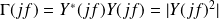Spectral Analysis

Lesson

Power Spectral

Power spectral density function (PSD) shows the strength of the variations(energy) as a function of frequency. It shows at which frequencies variations are strong and at which frequencies variations are weak. The unit of PSD is energy (variance) per frequency(width) and you can obtain energy within a specific frequency range by integrating PSD within that frequency range. The PSD is a very useful tool if you want to know frequencies and amplitudes of oscillatory signals in time series data.

$E_{y(t)} = |Y(f)^2|$

The PSD is calculate using the auto-correlation function. The definition of the temporal average auto-correlation function of a signal 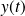in continuous time is:

$R(\tau) = \lim \limits_{T \rightarrow \infty} \frac{1}{2T} \int \limits_{-T}^{+T} y^*(t) y(t +\tau) dt$

Where is complex conjugation. This function measures at the time how the structures can be seen in a signal repeated over time scales of the order of .

Now, lets calculate the Fourier transform of the auto-correlation function:

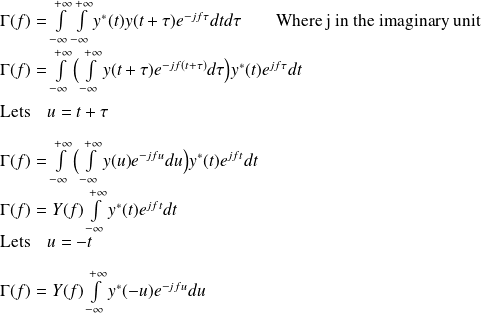
$\Gamma(f) = \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} y^*(t) y(t +\tau) e^{-jf\tau}dt d\tau \quad \quad \text{Where j in the imaginary unit}\\ \quad\\ \Gamma(f) = \int \limits_{-\infty}^{+\infty} \Big( \int \limits_{-\infty}^{+\infty}y(t +\tau) e^{-jf(t+\tau)} d\tau \Big) y^*(t) e^{jf\tau}dt \\ \quad\\ \text{Lets} \quad u = t + \tau\\ \quad\\ \Gamma(f) = \int \limits_{-\infty}^{+\infty} \Big( \int \limits_{-\infty}^{+\infty}y(u) e^{-jfu} du \Big) y^*(t) e^{jft}dt \\ \quad \\ \Gamma(f) = Y(f) \int \limits_{-\infty}^{+\infty} y^*(t) e^{jft}dt \\ \text{Lets} \quad u = -t \\ \quad\\ \Gamma(f) = Y(f) \int \limits_{-\infty}^{+\infty} y^*(-u) e^{-jfu}du$

The second rhs term is equal to 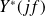, thus

Homepage