Cascade phenomenology

Lesson

Introduction
The matter of scale
Intermittency
- Introduction
- Intermittency visualization
- Intermittency quantification
- Multiplicative cascade
Discrete cascade
Other type of cascade
Exercises
To go further
Conclusion

Intermittency quantification

The intermittency can be quantified using the definition of the flatness. To this end, we use a high pass filtered signal 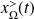defined as :

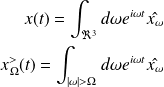
$\begin{eqnarray*} x(t) = \int_{\Re^3} d\omega e^{i \omega t} \hat{x_{\omega}} \\ x_{\Omega}^{>}(t) = \int_{|\omega| > \Omega} d\omega e^{i \omega t} \hat{x_{\omega}} \end{eqnarray*}$

We can say that the variable 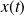is intermittent at small scales if the flatness grows without bound with the filter frequency .

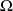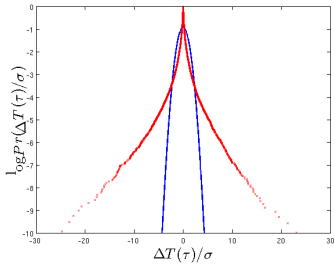
(red) : Probability density function of temperature increment, (blue) : Gaussian distribution

$\begin{equation*} F= \frac{S_4(l)}{\langle S_2(l) \rangle^2} = \frac{\langle (\delta T(l) )^4\rangle}{\langle (\delta T(l))^2 \rangle^2} \end{equation*}$

The flatness is useful measure of intermittency for signals having a bursty aspect. Instead of flatness it is possible to use other nondimensional ratios, such as the moment of order 6 divided by the cube of the second moment order.

Homepage