Source Of Complexity

Lesson

Navier-Stokes equations

The Navier-Stokes equations :

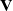$\frac{\partial \textbf{V}}{\partial t} + (\textbf{V}. \nabla).\textbf{V} = \frac{-1}{\rho} \nabla \textbf{P} + \nu \nabla^2 \textbf{V} + \textbf{F}$

is the velocity vector field.

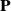is the pressure

is the kinematic viscosity

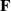represents the external forces

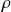is the density of the fluid

There are two ways to understand why the Navier-Stokes is complicated: mathematical vision and physical vision. For the mathematician, the equation is complicated because it is a non-linear differential equation. For the physician this nonlinear term its translation into the complexity of the described physical phenomena which is the turbulence which is the physical equivalent of the non-linearity of the Navier-Stokes equation.

The researchers of the 19th century began with seeking analytical solutions to the equations: explicit formulas for a solution based on equations considered. They quickly realized the difficulty of obtaining exact analytical solutions. Showing that the equations are well posed:

Existence: if we experience, can be seen (as long as you like).

Uniqueness: if it is done twice, one must observe the same.

Stability: if one approximates the data or the equation, the solution should not be too changed.

Homepage